Sobat pernah lihat mesin giling ataupun roda sepeda? Bila sobat lihat lagi di sepeda terdapat rantai yang menghubungkan antara gear roda dengan gear pedal. Nah dua roda gear itulah yang disebut dua lingkaran dan rantai itu desebut garis singgungnya. Lebih tepatnya garis singggung persekutuan luar. Jadi dapat diartikan bahwa garis singgung lingkaran adalah garis yang tepat menyinggung dua lingkaran.
1. Garis Singgung Persekutuan Luar
Panjang Garis Singgung Persekutuan Luar Lingkaran
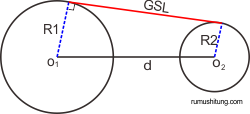
- Lingkaran besar dengan pusat O1 dan jari-jari R1
- Lingkaran kecil dengan pusat O2 dan jari-jari R2
- d = jarak antara dua titik pusat lingkaran (antara O1 dan O2)
- GSL = Garis Singgung Persekutuan Luar Lingkaran.
Dari mana sih asal rumus tersebut? Coba sobat amati gambar berikut,
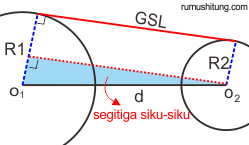
Rumus mencari garis singgung dua lingkaran (garis persekutuan) sebenarnya berasal dari aturan phytagoras, Lihat segitiga siku-siku berwarna biru. Dengan segitiga itu kita bisa menghitung panjang garis GSL dengan phytagoras d(O1-O2) dan Selisih jari-jari lingkaran besar (R2) dengan jari-jari lingkaran kecil. maka didapatlah persamaan rumus garis singgung dua lingkaran seperti ini
R1-R2 = seisih jari-jari.
Lalu bolehkah dibalik menjadi R1-R2?
Boleh karena pada prinsipnya bilangan negatif dan positif kuadratnya akan selalu positif. Sobat harus hati-hati dengan tanda negatif (-) dan Positif (+).
2. Garis Singgung Persekutuan Dalam
Panjang Garis Singgung Persekutuan Luar Lingkaran =
Dari mana asal rumus tersebut? Sama seperti pada garis singgung lingkaran luar, ini hanya aturan phytagoras. Lihat gambar di bawah ini
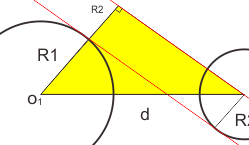
Lihat segitiga yang berwarna kuning. Kelihatan kan dari mana asal rumusnya. Yap, dari phytagoras antara d (jarak antar pusat lingkaran) dengan jumlah R1 dan R2. So didapatlah rumus seperti yang diatas.
Buah sobat hitung, ini ada cara menghafalnya..
DALAM = TAMBAH (sama-sama ada M)
LUAR = KURANG (sama-sama ada R)
Semoga cara tersebut bisa memudahkan mengingat rumus garis singgung dua lingkaran. Sekian sobat, semoga bermanfaat.
Posting Komentar